#Ein Weihnachts-Krypto-Rätsel vom britischen Nachrichtendienst GCHQ – Klausis Krypto Kolumne

English translation (Beta)

Bereits Anfang 2016 habe ich über ein Weihnachtsrätsel gebloggt, das die britische Sicherheits- und Nachrichtendienst-Behörde GCHQ veröffentlicht hat.

Das GCHQ

Damals spielten Schachfiguren eine wichtige Rolle, und die Sache war wohl ziemlich schwierig.

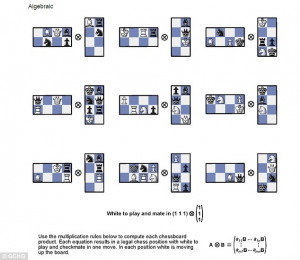
Quelle/Source: GCHQ

Das GCHQ ist quasi das britische Gegenstück zur US-amerikanischen NSA. Ihr Hauptquartier in Cheltenham im Südwesten Englands muss einen Vergleich mit dem Vorbild jedenfalls nicht scheuen.

Quelle/Source: Wikimedia Commons

Direkt neben diesem als “Donut” bezeichneten Gebäude stehen übrigens die Listening Stones von Gordon Young.

Quelle/Source: Schmeh

Zwei dieser neun Skulpturen tragen eine verschlüsselte Inschrift. Selbstverständlich ist dieser Ort in meinem (mit Christian Baumann entwickelten) Cryptologic Travel Guide gelistet.

Weihnachtsrätsel 2020

Blogleser Jan Stauffacher hat mich dankenswerterweise darauf hingewiesen, dass das GCHQ vor ein paar Tagen wieder ein Weihnachtsrätsel veröffentlicht hat. Aus urheberrechtlichen Gründen kann ich hier nur eine gepixelte Version vorstellen:

Quelle/Source: GCHQ

Hier geht es zum Original.

Wie man sieht, stehen unten auf dem Blatt neun Buchstabengruppen. Die Gruppe unten rechts kann man als römische Zahl 1665 interpretieren, die anderen ergeben keinen erkennbaren Sinn.

Oben ist ein Labyrinth (mathematisch gesprochen: ein Graph) mit neun Räumen (mathematisch gesprochen: Knoten) abgebildet.

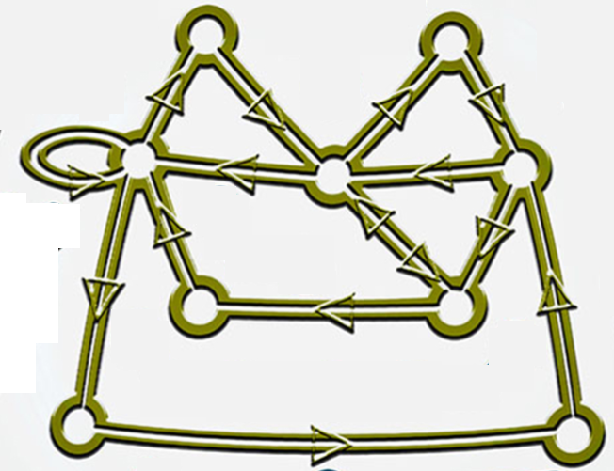
Quelle/Source: GCHQ

Es gibt (mindestens) einen Weg, der alle Verbindungsgänge genau einmal in Pfeilrichtung enthält und danach wieder am Ausgangsraum angelangt. Dies bezeichnet man in der Mathematik als Eulerkreis. Der Start-/Zielraum ist, soweit ich sehe, nicht festgelegt. Man kann also überall anfangen und gelangt am Ende wieder dorthin.

Die neun Buchstabengruppen unten auf dem Blatt sind wie die neun Räume oben angeordnet. Ich vermute daher, dass jede Gruppe einem Raum zugeordnet ist. Vermutlich muss man dem Eulerkreis folgend von einer Buchstabengruppe zur nächsten gehen und dabei jeweils einen Buchstaben auswählen.

Weiter bin ich bisher nicht gekommen. Findet ein Leser die Lösung zu dieser Knobelei?
Follow @KlausSchmeh

Further reading: Vom Teddybär bis zum Weihnachtsbaum-Anhänger: die schönsten Merchandising-Produkte der NSA

Linkedin: https://www.linkedin.com/groups/13501820
Facebook: https://www.facebook.com/groups/763282653806483/