#Theorema Magnum MCMXLIII: stetiger Funktionalkalkül – Mathlog

Die Lösung der linearen Differentialgleichung x‘(t)=Ax(t) im Rⁿ mit einer nxn-Matrix A ist bekanntlich x(t)=e^tAx(0), wobei das Matrixexponential e^tA definiert ist als die Reihe . (Matrizen können addiert und miteinander und mit Skalaren multipliziert werden, was zunächst Polynome von Matrizen definiert. Es ist dann nicht schwer zu zeigen, dass die Matrizenfolge konvergiert.)

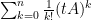
Dagegen läßt sich der Logarithmus einer beliebigen Matrix nicht einfach durch die Potenzreihe definieren, denn diese konvergiert nicht für jede Matrix. Für eine Diagonalmatrix etwa konvergiert sie genau dann, wenn ihr Spektrum zum Konvergenzbereich der ln(1+x) definierenden Potenzreihe gehört.
Gegeben eine Funktion f, ist es offensichtlich eine notwendige Bedingung für eine sinnvolle Definition einer Matrix f(A), dass die Funktion f zumindest auf dem Spektrum von A definiert sein muß. (Als Spektrum eines Operators bezeichnet man die Menge der komplexen Zahlen λ, für die λ.id-A nicht invertierbar ist. Ende der 30er Jahre bewiesen Gelfand und Mazur, dass das Spektrum jedes Operators nicht leer ist.)
Für normale Matrizen ist diese Bedingung auch hinreichend, weil sie sich diagonalisieren lassen und für Diagonalmatrizen die Einträge zum Spektrum gehören, auf dem sich f anwenden läßt.
Der Versuch, diesen Ansatz von endlich-dimensionalen Matrizen auf Operatoren zwischen unendlich-dimensionalen Vektorräumen zu verallgemeinern, führt auf verschiedene Funktionalkalküle.

Beim stetigen Funktionalkalkül möchte man Operatoren in (zumindest auf dem Spektrum definierte) stetige Funktionen einsetzen. Für die von einem Operator A und seinem Adjungierten A* (im Fall von Matrizen ) erzeugte Algebra B sucht man also nach einem Homomorphismus C(Spek(A))—->B, der den auf dem Spektrum von A definierten stetigen Funktionen f einen Operator f(A) zuordnet, so dass Spek(f(A))=f(Spek(A)).
Der naheliegende Ansatz beginnt natürlich mit Polynomen, in die man Operatoren auf die offensichtliche Weise einsetzen kann. Stetige Funktionen sind zwar im Allgemeinen keine Potenzreihen, sie lassen sich aber jedenfalls nach dem Satz von Stone-Weierstraß durch Polynome approximieren. Die Frage ist dann, ob die entsprechende Folge von Operatoren gegen einen Operator konvergiert. Diese Frage führte zur Theorie der C*-Algebren.

Israel Gelfand war Student Kolmogorows gewesen, hatte 1938 im Alter von 25 Jahren über kommutative normierte Algebren habilitiert und war 1941 auf einen Lehrstuhl an der Moskauer Staatsuniversität befördert worden. Zwei Jahre später gründete er sein Forschungsseminar zur Funktionalanalysis.
Mit Naimark bewies er 1943 einen Satz, der zum Ausgangspunkt der Theorie der C*-Algebren werden sollte.
C*-Algebren sind Banach-Algebren (vollständige normierte Algebren mit submultiplikativer Norm), für die es eine anti-multiplikative, konjugiert-lineare Involution * mit für alle a gibt. (Aus dieser Gleichung folgt, dass die Involution isometrisch ist.)
Das einfachste Beispiel ist die Algebra C₀(X) der komplex-wertigen, im Unendlichen verschwindenden, stetigen Funktionen auf einem lokalkompakten topologischen Raum X. Diese Algebra ist kommutativ. Gelfand und Naimark bewiesen, dass man jede kommutative C*-Algebra A als C₀(X) für einen lokalkompakten Raum X (den man sogar Hausdorffsch wählen kann) bekommt. Man kann für X nämlich die Menge aller von der Nullabbildung verschiedenen *-Homomorphismen von A in die komplexen Zahlen (oder äquivalent die Menge aller maximalen Ideale in A) mit einer geeigneten Topologie wählen.

Dieser Satz ermöglichte die Übersetzung algebraischer Eigenschaften kommutativer C*-Algebren in topologische Eigenschaften lokalkompakter Räume. Die Algebra A hat ein Einselement genau dann, wenn X kompakt ist. Die Adjunktion eines Einselements entspricht der Einpunktkompaktifizierung. Die Algebra ist endlich erzeugt genau dann, wenn X Teilmenge eines endlichdimensionalen Vektorraums ist. Die Algebra ist separabel genau dann, wenn X dem zweiten Abzählbarkeitsaxiom genügt.

Die zunächst interessantere Anwendung war aber der stetige Funktionalkalkül. Im Allgemeinen hat man für Banach-Algebren nur einen holomorphen Funktionalkalkül, d.h. für holomorphe auf dem Spektrum eines Elements a definierte Funktionen f kann man f(a) definieren. Für C*-Algebren bekommt man aber mit der Arbeit von Gelfand-Naimark sogar einen stetigen Funktionalkalkül, also ein Element f(a) schon für stetige Funktionen auf dem Spektrum des Elements a.
Wenn nun N ein beliebiger normaler Operator auf einem Hilbertraum ist, dann ist der Abschluß der von N und N* erzeugten Operatorenalgebra eine kommutative C*-Algebra E(N,N*), auf die man die Konstruktion von Gelfand-Naimark anwenden kann. Der im Beweis des Satzes von Gelfand-Naimark konstruierte Raum X ist gerade das Spektrum von N. Der Satz von Gelfand-Naimark gibt also eine Isomorphismus , der die Inklusion auf N abbildet; das ist also der gewünschte Funktionalkalkül nicht nur für Potenzreihen, sondern allgemein für stetige Funktionen.