#Theorema Magnum MCMXXXIV: Pontrjagin-Dualität – Mathlog

Viele Differentialgleichungen lassen sich mit dem Ansatz lösen, die gesuchte Funktion in Schwingungen (periodische Funktionen) unterschiedlicher Frequenz zu zerlegen. Diese Methode heißt Fourier-Analyse: man schreibt eine 2π-periodische Funktion F(x) als F(x)=f(e^ix), also als Funktion f:S¹—->C, und entwickelt sie in eine Fourier-Reihe f(e^ix)= Σ a_ne^inx (oder äquivalent in eine Reihe mit Summanden cos(nx) und sin(nx)). Die Koeffizienten kann man berechnen durch . Die Zuordnung n–>a_n ist eine Folge, also eine Funktion Z—->C. Fourierentwicklung gibt also eine Zuordnung zwischen Funktionen auf S¹ und Funktionen auf Z, eine Dualität zwischen Z und S¹.
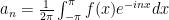
Pontrjagin-Dualität liefert die Verallgemeinerung dieser Theorie auf beliebige lokalkompakte, abelsche Gruppen. Zu einer solchen Gruppe G betrachtet man die duale Gruppe (äquivalent: die Gruppe der irreduziblen Darstellungen) und kann dann jeder Funktion die Fourier-Transformierte zuordnen, womit man eine zur Fourier–Analyse analoge Theorie erhält.

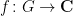
Pontrjagin hatte als 14-jähriger bei der Explosion eines Gasofens sein Augenlicht verloren. Dank seiner Mutter, die ihm neben ihrer Arbeit als Näherin mathematische Bücher und topologische Arbeiten vorlas, machte er trotzdem Karriere. Noch als Student bewies er die allgemeine Version der Alexander-Dualität von Homologiegruppen: für eine abgeschlossene Teilmenge hat man einen Isomorphismus für eine kompakte Gruppe G und ihr (diskretes) Dual, also die Gruppe aller irreduziblen Darstellungen, im abelschen Fall einfach . (Mit Alexander-Dualität kann man beispielsweise für einen Knoten unmittelbar die Homologiegruppen des Knotenkomplements berechnen, die insbesondere also nicht vom Knoten abhängen. Alexander hatte diesen Dualitätssatz für endliche Polyeder bewiesen, Alexandrow dann auf abgeschlossene Mengen verallgemeinert. Beide hatten aber nur Koeffizienten betrachtet.)
Pontrjagin formulierte auch als erster ein allgemeines Prinzip, in das alle bekannten topologischen Dualitätssätze paßten: wenn es zu zwei abelschen Gruppen A und B eine Abbildung AxB—->C in eine endliche zyklische Gruppe C oder in die reellen Zahlen gibt, die ein Homomorphismus in beiden Argumenten ist und nicht-ausgeartet ist, d.h. zu jedem von Null verschiedenen Element aus A oder B existiert ein Element aus der anderen Gruppe, so dass das Paar nicht auf Null abgebildet wird, dann ist B dual zu A. (Im Nachhinein liegt das daran, dass Z/mZ und R jeweils zu sich selbst Pontrjagin-Dual sind.)
Damit erhält man zum Beispiel Poincaré-Dualität, indem man für die freien Anteile A von H_k(M;Z) und B von H_n-k(M;Z) die Schnittzahl und für die Torsionsanteile die Torsionsverschlingungszahl betrachtet. Ähnlich bekommt man Lefschetz-Dualität, also die Verallgemeinerung der Poincaré-Dualität auf Mannigfaltigkeiten mit Rand. Die Alexander-Dualität bekommt man, indem man die Verschlingungszahl betrachtet.

Bekannt wurde er aber dann aber für eine andere Dualitätstheorie, die mit den topologischen Dualitätssätzen nur insofern zu tun hatte, dass man für die Koeffizienten der Alexander-Dualität jeweils die in diesem Sinne duale Gruppe braucht. (Was allerdings seine ursprüngliche Motivation zur Entwicklung dieser Dualitätstheorie war.) 1934 entwickelte er die später als Pontrjagin-Dualität bezeichnete abstrakte Theorie der Fourier-Analyse. Diese Theorie funktioniert für lokalkompakte, abelsche Gruppen G und für die mit Homomorphismen nach S¹ gebildete duale Gruppe. (Die Homomorphismen nach haben S¹ wie Homomorphismen nach R und anders als Homomorphismen nach Z die Eigenschaft, dass sich Homomorphismen einer Untergruppe von G auf ganz G fortsetzen lassen, was für Beweise zentral ist.)
Die duale Gruppe wird mit der schwächsten Topologie versehen, für die die durch gegebene Transformation noch stetig ist.
Lokale Kompaktheit der Gruppe G ist notwendig, weil die Konstruktionen und Beweise ein invariantes Maß auf der Gruppe benötigen. Die Existenz und (bis auf Skalierung mit Konstanten) Eindeutigkeit eines invarianten Maßes μ_G auf einer lokalkompakten Gruppe G hatte Alfréd Haar in einer 1933 zwei Monate vor seinem Tod in Annals of Mathematics erschienenen Arbeit „Der Massbegriff in der Theorie der kontinuierlichen Gruppen“ bewiesen.